Skip to main content

MonadBFT

Summary​

MonadBFT represents a major leap in Byzantine Fault Tolerant (BFT) consensus. It is responsible for ensuring that the Monad network aligns on valid proposed blocks efficiently and securely, while supporting 10,000+ tx/s and sub-second time-to-finality, while also supporting a large consensus node set.

MonadBFT combines all of these properties while also being resilient to tail-forking, a critical weakness of pipelined leader-based BFT protocols where a leader can fork away its predecessor's block.

For a full description and deep technical dive into MonadBFT, please refer to the full research paper, the latest blog post from Category Labs and the original blog post introducing MonadBFT.

MonadBFT achieves:

  • Speculative finality in a single consensus round, and full finality in two rounds.
  • Linear message and authenticator complexity on the happy path (meaning under normal operations, when no failures occur). This allows the consensus validator set to scale to a large number of nodes.
  • Optimistic responsiveness: round progression without waiting for the worst-case network delay, both in the common case and while recovering from failed rounds.
  • Leader fault isolation A single failed leader only incurs one timeout delay. All other rounds are able to proceed as quickly as the network allows. This is in contrast to existing pipelined BFT protocols, which have a two timeouts for a failed leader.
  • Tail-forking resistance: built-in protection against tail-forking, a class of Maximal Extractable Value (MEV) attacks where a malicious leader could otherwise fork away its predecessor's block. This resolves a critical issue in prior pipelined leader-based BFT consensus mechanisms.

No other pipelined leader-based BFT protocol combines all these features.

note

Category Labs has made several recent improvements to MonadBFT. This page and the research paper have now been updated with full details. Find out what's new in the Fast Recovery section or by reading this blog post.

Configuration in Monad​

Sybil resistance mechanismProof-of-Stake (PoS)
Min block time400 ms
Finality2 slots (800 ms)
Speculative finality (can only revert in rare circumstances requiring equivocation by the original leader)1 slot (400 ms)
Delegation allowedYes

Demo​

See this blog post from Category Labs for a live demo of MonadBFT!

The demo runs the exact implementation of monad-bft that powers the live Monad blockchain, compiled to Wasm and run in your browser against a simulation framework (mock-swarm).

Common Concepts​

To explain MonadBFT, it helps to define a few concepts first. We will start with some concepts common to many BFT mechanisms:

Byzantine threshold​

As is customary, let there be n = 3f+1 nodes, where f is the max number of Byzantine (faulty) nodes. That is, 2f+1 (2/3) of the nodes are non-Byzantine. In the discussion below, we treat all nodes as having equal stake weight; in practice all thresholds can be expressed in terms of stake weight rather than in node count.

Supermajority​

>2/3 of the stake weight.

Round​

The protocol proceeds in rounds, also referred to as views. The round number increases by 1 with each step of the protocol regardless of whether a block proposal is successfully made.

Leader​

Each round has one leader who has the authority to make a block proposal. The leader rotates each round according to a schedule determined previously using the stake weights.

Block​

A block consist of a round number, a payload (an ordered list of transactions), and a QC. A block builds on a parent block, and includes a QC certifying that parent block. Blocks are chained together via the parent relationship, which is why we called it a blockchain.

Quorum Certificate (QC)​

Validators evaluate the validity of each block proposal and send their votes to the next leader. If the next leader receives a supermajority of YES votes, they aggregate those votes into a Quorum Certificate (QC) on that block proposal. A QC is proof that 2/3 of the network received and voted YES on a block proposal.

Although this is more of an implementation detail, it is worth noting that in Monad's implementation of MonadBFT, validators sign with BLS signatures because those signatures can be efficiently aggregated, making signature verification on the QC relatively inexpensive.

Linear communication​

Each round follows a fan-out fan-in pattern. The leader sends their block proposal to each validator (using RaptorCast for efficient broadcast). Validators evaluate the block proposal and send a signed vote directly to the next leader. This linear communication mechanism contrasts with other protocols which rely on all-to-all (quadratic) communication; it allows the consensus set to scale.

Concepts relatively unique to MonadBFT​

The following are concepts that are relatively unique to MonadBFT. We are splitting them out to aid in comprehension. For simplicity, we focus on the standard recovery in MonadBFT. The fast recovery optimizations are explained in the Fast Recovery section.

Proposal​

A block proposal (often just called proposal) consists of the current round number, a block, an optional TC or NEC, and a signature (from the leader making the proposal) over the previous elements. In the simple case, optional fields are blank and the round number is the same as the block's round number, such that the proposal is basically a signed block. Sometimes, a block that failed to get traction gets reproposed; in that case, the block will still have the round number from when it was first proposed, but the proposal will have the round number of when it is reproposed.

Fresh Proposal​

A fresh proposal is a proposal containing a new block, i.e. one that is not influenced by prior failed proposals.

A fresh proposal will either:

  1. have a round number that is equal to its QC's round number plus 1. This is the common case, when leaders are honest and online, and the network does not have any abnormal delays.
  2. have a TC identifying a high QC. This happens when a leader recovers from a failed round (fast recovery).
  3. have a NEC. This happens very rarely, when a leader recovers from a more complex failure (standard recovery).

Reproposal​

A reproposal is a proposal containing a block from a previous fresh proposal that the current leader is trying to revive or finalize. A reproposal will have a round number greater than its QC's round number plus 1.

Whether a leader recovering from a failure has to repropose a previous block or not is determined by the TC. If the TC contains a high tip (instead of a high QC), then the block corresponding to the high tip must be reproposed. Reproposals are part of the standard recovery. In practice, reproposals can often be skipped with fast recovery.

Tip​

A tip is a proposal minus the block's payload. You can think of it as the block header of the proposal plus a bit of extra metadata, including the round number that that proposal was received.

In MonadBFT, every validator keeps track of its latest tip, which is updated whenever the validator votes for a proposal. If the validator votes for a reproposal, the tip is set to the original proposal, not its reproposal.

High Tip​

Given a set of tips, high tip is just the tip with the highest round number. If there are multiple such tips, then the tip that builds on the highest QC embedded in it is chosen.

Timeout Message​

A timeout message is a signed attestation that a validator produces when it hasn't received a valid block from the scheduled leader in the expected time. The timeout message attests to the lack of a valid block.

Each validator sends the timeout message to all other validators, utilizing all-to-all communication.

Timeout messages are utilized in other BFT protocols. In MonadBFT, timeout messages include the sender's tip - additional information about their view of the world which will be utilized in MonadBFT to recover gracefully from the timeout. For fast recovery, the timeout message contains the validator's highest QC, if it is of equal or higher view than the view of the local tip.

Timeout Certificate (TC)​

When a timeout occurs, validators start sending and receiving timeout messages. Each validator accumulates the timeout messages that it receives; if it gets to a supermajority of such messages, it builds a Timeout Certificate (TC).

The TC includes information on all of the tips from all of the validators contributing timeout messages. The high tip (for standard recovery) is also computed. In most cases, fast recovery is possible, and the TC contains a high QC instead of a high tip.

No-Endorsement Message and No-Endorsement Certificate​

Under certain conditions, a leader will ask the other validators for the full proposal (block) corresponding to a tip. If the validator doesn't have it, they will respond with a signed No-Endorsement Message attesting to this.

If the leader gets a supermajority of No-Endorsement Messages when trying to recover the proposal of a tip, they can produce a No-Endorsement Certificate - proof that a supermajority of the network didn't have that proposal.

Block states due to MonadBFT​

Blocks can be in one of three states due to MonadBFT:

  1. Proposed
  2. Voted
  3. Finalized

These are three of the four states that blocks can be in overall within Monad, as mentioned in Block States. (The fourth state, Verified, is achieved outside of MonadBFT as a part of Asynchronous Execution.)

Below, we describe how blocks progress through these states.

Happy Path​

The happy path describes the ordinary case of how a block goes from being proposed to being finalized without any timeouts or failed rounds.

Scenario​

To describe the flow of the happy path, we'll follow the scenario shown in the diagram below.

It is currently round K and the scheduled leader is Alice. Bob and Charlie are the next two leaders in the schedule. Alice has last seen block N-1, so she is going to propose block N.


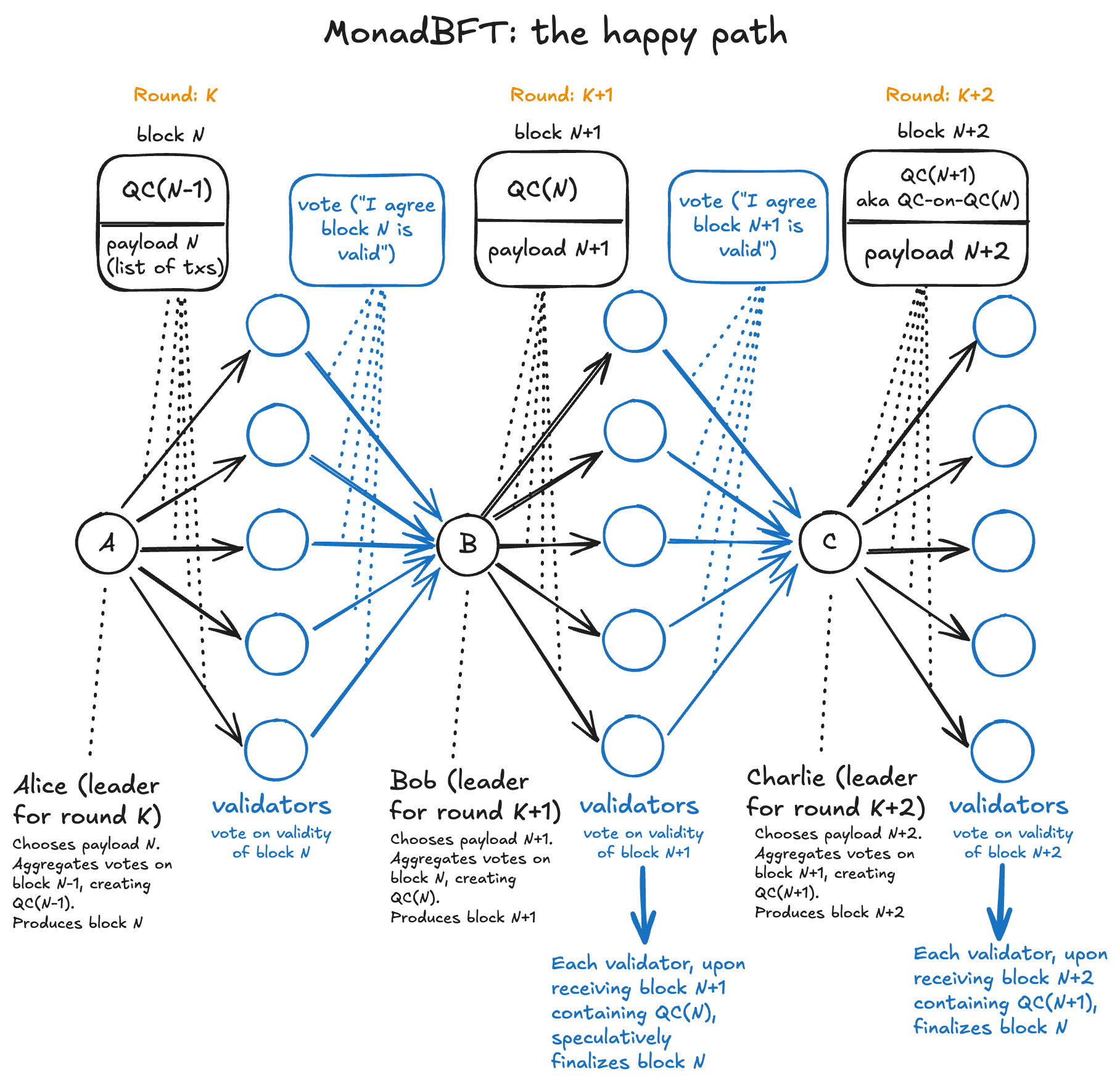
MonadBFT proceeds as follows.

Round K: Alice's proposal​

  1. Proposal: Alice, the designated leader for round K, chooses a payload, i.e. a list of transactions chosen from her mempool. She builds block N, consisting of the payload and a QC from the previous proposal (don't worry about this part). Alice sends the proposal consisting of that block directly to all other validators.

  2. Voting: Each validator checks Alice's proposal for validity. If the proposal is valid, the validator sends signed votes directly to Bob, the designated leader for round K+1, and marks block N as Proposed.

  3. QC Formation: Upon getting a supermajority of votes about Alice's proposal, Bob aggregates the votes into a QC about Alice's proposal.

Round K+1: Bob's proposal​

  1. Proposal: Bob chooses a payload. Bob combines the payload with the QC from Alice's proposal to produce a new block, which he sends to all other validators.

  2. Voting: Each validator checks Bob's proposal for validity. If the proposal is valid, the validator sends votes directly to Charlie, the designated leader for round K+2, and marks block N as Voted (and block N+1 as Proposed.)

    This also means that the block can be speculatively finalized. This speculative finality will only revert under very specific rare conditions, which also come with accountability. More on this later.

  3. QC Formation: Upon getting a supermajority of votes about Bob's proposal, Charlie aggregates the votes into a QC about Bob's proposal. This QC can also be thought of a QC-squared on Alice's proposal, since it is a QC attesting to the fact that a supermajority received the QC about Alice's proposal.

Round K+2: Charlie's proposal​

  1. Charlie's proposal: As before, Charlie builds a block, consisting of a new payload and the QC on Bob's proposal. Charlie sends the proposal to everyone.

  2. Voting: Each validator checks Charlie's proposal for validity. If the proposal is valid, the validator sends votes directly to David, the designated leader for round K+3, and marks block N as Finalized (and block N+1 as Voted and block N+2 as Proposed.)

Although we will stop describing the sequence at this point, the consensus mechanism continues repetitively. As soon as each validator receives David's proposal (which contains a QC about Charlie's proposal aka a QC-squared about Bob's proposal), they can mark Bob's proposal as Finalized (and Charlie's as Voted). And so on.

This underscores the pipelining aspect of MonadBFT. Every round, a new payload and a new QC about the previous proposal gets shared, allowing the parent proposal to be speculatively finalized and the grandparent proposal to be fully finalized. You can see this here:

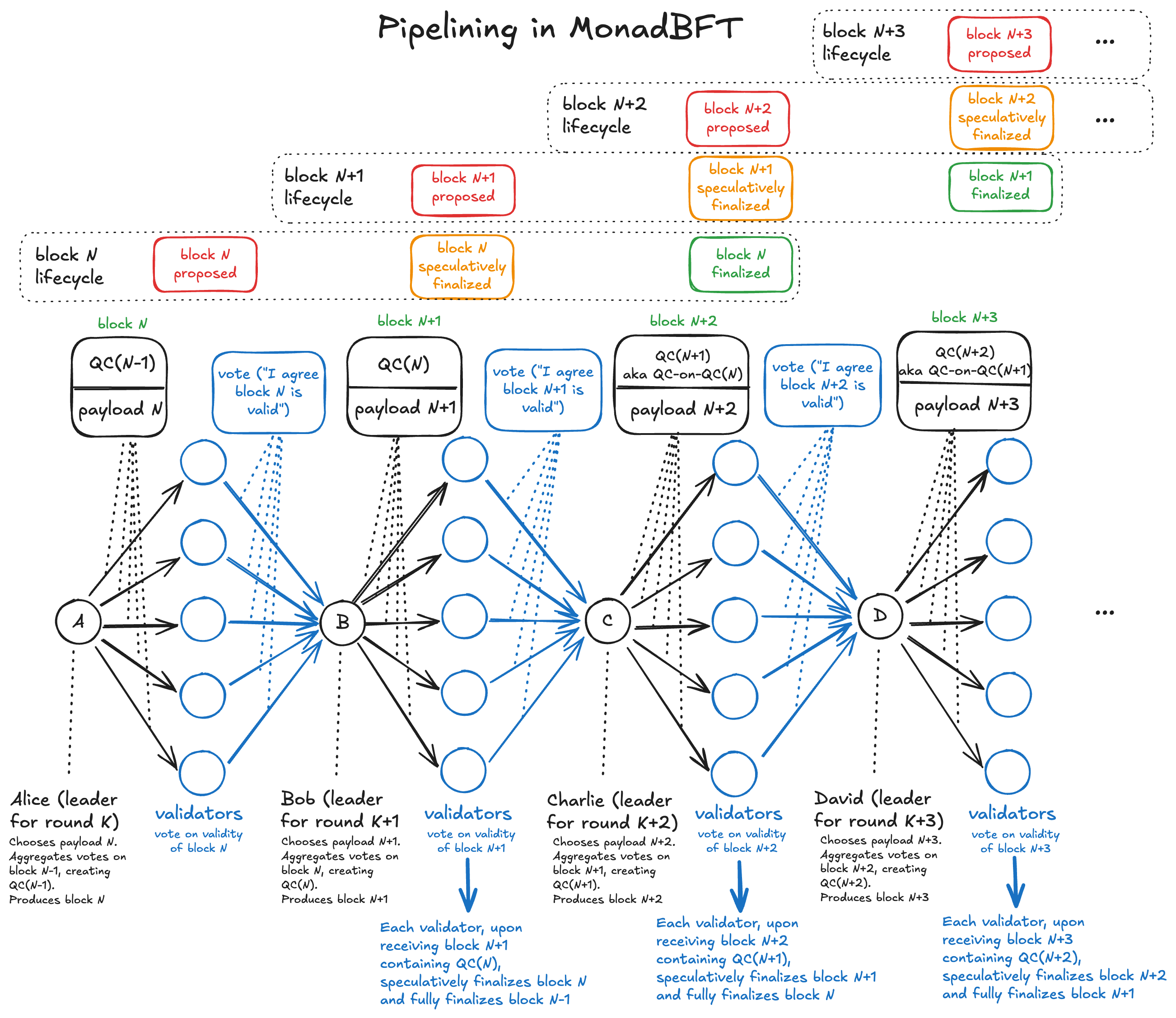
Illustrating the pipelined (staggered) nature of MonadBFT. Same diagram as the previous, but zoomed out to include one more round.

Unhappy Path (Fault Handling)​

The unhappy path describes the abnormal case where either the leader fails to send out a valid proposal or the QC builder (next leader) fails to build a QC.

Understanding the unhappy path is crucial to understanding how the happy path works as well! The thing that ultimately allows a validator to speculatively finalize a proposal after receiving the child proposal, or finalize a proposal after receiving the grandchild proposal, is knowing that the fallback mechanism will still preserve the original proposal.

Here, we will focus on the standard recovery, which is actually the fallback of the fallback mechanism. In most cases in practice, we can use fast recovery, which substantially speeds up the time for the protocol to go back to the happy path after a failure occurs. However, for the protocol as a whole to achieve the tail forking resistance, even in the worst case of Byzantine failures, we rely on the standard recovery, which we now present.

Scenario​

As before, to describe the flow of the unhappy path, we'll follow a scenario shown in a diagram.

Again, suppose that it is currently round K and Alice is the scheduled leader. Bob and Charlie are the next two leaders in the schedule. Alice has last seen block N-1, so she is going to propose block N.

In our example, Alice sends block N at round K, but Bob fails to send a block at round K+1. This could be because he was offline, or it could be that Alice either sent an invalid block, or not enough people voted for it.

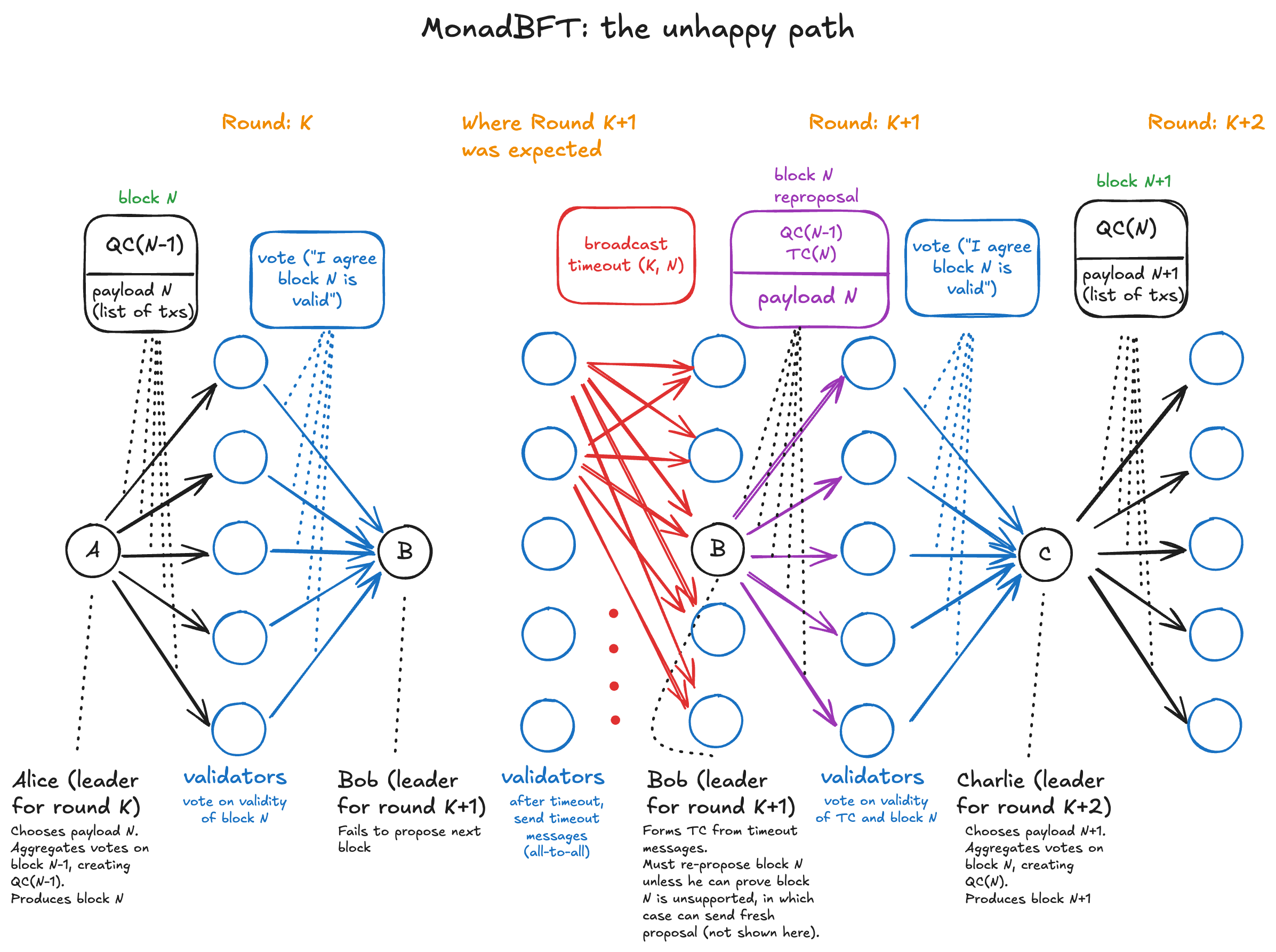
Round K: Alice's proposal​

  1. Proposal: Alice, the designated leader for round K, chooses a payload and builds block N, consisting of the payload and a QC from the previous proposal (again, don't worry about this part).

    Alice sends the proposal directly to all other validators.

  2. Voting: Each validator checks the proposal for validity and, if valid, sends signed votes directly to Bob, the designated leader for round K+1. Each validator marks Alice's proposal locally as Proposed.

When round K+1 was expected: Bob's missed slot​

  1. Bob fails to propose block N+1, so all votes are blackholed and no QC for Alice's block is produced.

  2. Everyone sends timeout messages: After a timeout window, each validator "realizes" that round K has failed since no QC is formed for Alice's block. Therefore, everyone sends a timeout message about block K to every other validator. (Note that this communication is all-to-all.)

  3. TC assembly: Upon getting a supermajority of timeout messages, every validator including Bob assembles a TC, proving that round K (Alice proposer, Bob QC builder) failed. Upon building a TC for K, validators advance their round to K+1.

Round K+1, as progressed by TC​

The TC contains a computed value called high_tip, which (roughly speaking) is the block header of the latest valid block that any of the validators contributing to the timeout message have seen. You can think of high_tip as the max block observed over the 2/3 of the stake weight required to sign the TC.

In this specific example, high_tip will be the block header of Alice's block.

Under the rules of MonadBFT, the next leader is obligated to either re-propose the block referenced in high_tip of the TC (i.e. Alice's block), or to prove that that block is unsupported. (We'll discuss this in more detail below.)

Since we are now in Round K+1, the next leader is Bob. (You might find this ironic, but it is a necessary consequence of the fact that the protocol cannot distinguish between the possibility that Bob was offline, and the possibility that either Alice sent an invalid block or not enough people voted on Alice's block. In either of the latter cases, it would be unfair to skip Bob.)

  1. (Optional) Requesting Alice's block from other validators: Bob needs to re-propose Alice's block. However, the high_tip is only a block header - not the full block body - so if Bob doesn't have Alice's block, he can request the full version from the other validators (via blocksync).

Reproposal case (Bob re-proposes Alice's block)​

  1. Reproposal: If Bob has Alice's block (either due to already receiving it when he originally proposed it, or via blocksync) then he proposes it along with the TC justifying the re-proposal.

  2. Voting: Each validator votes on the validity of Bob's reproposal. If the reproposal is valid, validators send their votes to the next leader, Charlie.

  3. QC Formation: Charlie assembles a QC from the votes.

  4. Charlie's proposal: Charlie builds a block at round K+2, consisting of a new payload and the QC on reproposal from round K+1, and sends the block to everyone. At this point Alice's block becomes Voted to anyone who receives Charlie's block. Everyone advances their rounds to K+2 and the protocol returns to the happy path.

Fresh proposal case (Bob proves Alice's block is unsupported)​

  1. No-Endorsement of Bob's block: Recall that in step 6, Bob was allowed to poll the other validators for Alice's block. When a validator is polled, if they also don't have it, they can send Bob a signed No-Endorsement Message attesting to not having seen Alice's block. If a supermajority of the validators sign No-Endorsement Messages, then Bob may assemble a No-Endorsement Certificate (NEC).

  2. Bob's fresh proposal: Under the rules of MonadBFT, Bob may skip re-proposing Alice's block, and instead make a fresh proposal of a new block (at the same block height N) if he can also supply a NEC.

    It's important to emphasize that Bob is only allowed to skip reproposing Alice's block if a supermajority of validators sign the NEC. Otherwise, he is obligated to re-propose. This rule helps ensure that Alice's block finalizes even though Bob failed to build a QC for Alice's block.

    From this point, consensus proceeds normally, returning to the happy path.

No proposal case​

There is a third possibility, which is that Bob fails to propose anything at all in round K+1. (This is fairly likely, because he failed to send a block the first time that round K+1 was expected.) In this case, a timeout occurs again, this time of round K+1, allowing consensus to move to round K+2, Charlie's turn. Charlie then inherits the situation Bob was in in round K+1, i.e. he must either re-propose Alice's block, or prove that Alice's block is unsupported.

More generally, if Charlie (and maybe a few subsequent leaders) also fail to propose anything, the situation will persist until someone either re-proposes Alice's proposal or proves that it is unsupported. That's the MonadBFT rule about the high_tip, and it ensures that Alice's block will eventually finalize unless it never should have been supported.

Discussion​

No-Tail-Forking​

In prior implementations of pipelined HotStuff-family consensus protocols, the case where Bob misses his slot results in Alice's proposal also being rolled back (tail forked). The intuition behind this is: Bob is the only person responsible for receiving everyone's votes on Alice's proposal, so when he goes offline, all of those votes are blackholed, making it hard to distinguish between the case where most validators voted YES for Alice's proposal and the case where most validators rejected her proposal.

For instance, in Fast-HotStuff, TCs carry enough information to prove that Bob missed his slot, allowing Bob to justifiably propose a block that skips Alice's block, making Alice's block a casualty. Bob simply re-proposes the same block height as Alice did, replacing Alice's block in the final blockchain. This is the reason why pipelined HotStuff consensus mechanisms prior to MonadBFT frequently see pairs of missed slots.

Tail forking is a serious weakness. When Alice’s block is proposed, if Bob sees valuable MEV opportunities in it, Bob—as QC builder (next leader)—may refuse to build the QC for Alice’s block and to propose his own block carrying Alice’s QC. In this case, validators cannot detect whether Alice failed to propagate her proposal or Bob refused to build a QC; therefore Bob is given an opportunity in round K+1 to propose a block. Bob can then extract high-value MEV by selecting only preferred transactions, and by reordering or replacing them at will. In other blockchains, unintentionally allowing blocks to be re-mined has resulted in massive impact.

The key to MonadBFT's No-Tail-Forking property lies in the handling of the missed slot situation. Intuitively speaking, in MonadBFT, TCs carry enough information to propagate the knowledge of the existence of Alice's block forward even when Bob blackholes all of the votes about it.

When it becomes Bob's turn to propose, he is obliged to re-propose Alice's block (based on the TC, which includes high_tip, aka a valid block header for Alice's block) unless he can get a supermajority (2f+1) to attest to not seeing Alice's block. The fact that a supermajority sign the NEC is key: even if f nodes are Byzantine, that still leaves f+1 non-Byzantine nodes attesting to not seeing Alice's block, which guarantees that Alice's block should not have achieved quorum since quorum requires 2f+1 votes and there were at least f+1 non-Byzantine NO votes.

The MonadBFT paper provides a far more robust definition of the protocol, and a formal proof that tail-forking cannot occur.

Speculative Finality​

The other extremely nice property of MonadBFT is one-slot speculative finality.

To explain this, it is first helpful to issue a reminder that a block's state is always from the perspective of a particular observer. For example, if you receive a QC for a block, then you can move that block to the Voted state, but if your friend didn't receive that QC yet, then she would still consider that block to be in the Proposed state.

The challenge of building a distributed consensus mechanism lies in defining rules that allow nodes to individually update their state machines in response to messages even while assuming the worst, i.e. even while assuming that they might be the only one that received that message.

After receiving Alice's Proposal​

Say that you are Valerie, one of the validators in the network. You receive Alice's proposal; you run the validity checks on it and they pass, so you mark Alice's proposal as Proposed.

Note that you don't know if anyone else has received this proposal, Alice could be being tricky and have only sent the proposal to you (or to a very small number of nodes) in an attempt to get you to diverge from everyone else.

After receiving Bob's Proposal​

Now say you receive Bob's proposal, which carries a QC for Alice's proposal. You run validity checks on Bob's proposal and they pass, so you mark Alice's proposal as Voted.

Again, although you now possess proof that a supermajority voted for Alice's proposal, you should be worried that Bob might be trying to trick you by only sending this to you. You should be worried that Bob's proposal doesn't reach quorum.

The superpower of MonadBFT is that, due to the complicated set of rules for handling a timeout described earlier, when you are in Valerie's position of having received Bob's proposal, you can mostly overpower that fear, at least as it pertains to the status of Alice's proposal. You may speculatively finalize Alice's proposal upon moving it to the Voted stage. That is, you can be confident that Alice's proposal will almost certainly end up being finalized, unless a very specific set of rare circumstances arises.

Intuitively, this makes sense given what we said above. You, Valerie, possess a QC for Alice's block, assembled by Bob. That actually means that, from your point of view, Bob was not offline.

And even if Bob were effectively offline to most people (e.g. he only sent the next proposal and QC-on-Alice's-block to you), you know that the procedure will be to assemble a TC; that the high_tip in that TC will probably point to Alice's block. Why? Because:

  1. the QC in your hands proves that a supermajority (2f+1) has seen Alice's block,
  2. the TC will also require a supermajority (2f+1)
  3. So at least f+1 voters will be common to both the QC and TC, and at most f are Byzantine, so at least 1 will reference Alice's block.

And if Alice's block makes it into high_tip, then Charlie will be forced to re-propose it (unless he could get a NEC on it, which he can't because that would require No-Endorsement Messages from a supermajority, when a supermajority already signed a QC on Alice's block).

So at first glance it seems like we, Valerie, might be able to finalize Alice's block as soon as we receive a QC on it.

The only loophole​

It turns out that there is one loophole which prevents us from being so confident. The loophole arises if Alice equivocated -- signed a second block b' at the same height as the first block b (which we have a QC for), and sent b' to a few nodes.

Under those circumstances, in the event where Bob sent his proposal only to us before going offline, then it is possible that high_tip in the resultant TC will resolve to b' instead of b. If that were to happen, then Charlie could end up either re-proposing b', or collecting an NEC on b' and using that to justify proposing a new block at Alice's block height.

In practice, this loophole is extremely rare for several reasons:

  1. Equivocation is an easily provable fault - all you need as evidence is both blocks at the same height both signed by Alice. Equivocation is a huge deal in blockchains, and can be severely punished.

  2. When Alice equivocates, she is only potentially disrupting herself (while also exposing herself to punishment for equivocation).

The MonadBFT paper provides a much more rigorous version of this argument. But in summary, locally observing a QC (moving a proposal to Voted) is a very strong indicator that the proposal will finalize, since the only way it won't is if Alice equivocated, Bob missed his slot, almost 1/3 of the network was Byzantine, and we still got quite unlucky with respect to which nodes ended up populating the TC.

Fast Recovery​

Since releasing the original MonadBFT paper in early 2025, Category Labs has analyzed the protocol’s behavior and designed, evaluated, and implemented several improvements. The protocol changes allow for fast recovery in the most common failure scenarios. This blog post gives a great introduction to how fast recovery works. In summary:

  • Validators now send their votes not only to the leader of the next view, but also to the leader of the current view. This gives each leader a chance to collect votes for its own proposal to form a QC, rather than relying solely on the next leader (who may be Byzantine). The leader broadcasts this QC.
  • Validators can include the highest QC that they have observed in their timeout message, instead of the tip. They do so if the QC is fresher (more recent) than the locally highest tip or produced in the same round as the tip.
  • If a validator sends a tip (instead of a high QC) in a timeout message, the validator also includes a tip vote, i.e., a vote for that tip with the current view number. 2f+1 votes for the same proposal in the same view, obtained via regular votes or timeout messages can be combined to form a new QC that can directly be extended by the next leader.
  • The timeout certificate includes the highest QC of the received timeout messages if it is at least as high as the highest tip. It also contains proof that the correct high tip or high QC was chosen. If the TC contains the high QC, then the leader can directly propose a fresh block extending that high QC.

These mechanisms enable faster recovery in the most common failure scenarios. For example, consider a situation where the leader in view v is offline. In the original MonadBFT protocol, this would cause views v-1 and v to time out (since the votes cast in v-1 are lost, and no block is proposed in view v). Additionally, the block proposed in view v-1 would have to be reproposed in view v+1, resulting in two consecutive views without a fresh block proposal.

With the updated protocol, several mechanisms enable faster recovery. For instance, in the timeout message of view v, each validator includes a tip vote for the block proposed in view v-1. This allows the leader of view v+1 to construct a QC in view v. Since no two conflicting QCs can be formed in the same view, the leader of v+1 can directly propose a fresh block extending this QC. As a result, a single crashed leader only causes the leader's view to time out; all other views succeed, and in each of them, a fresh block is proposed.

The other mechanisms similarly provide fast recovery options. We still retain the reproposal and NEC mechanisms from the original MonadBFT paper to address more complex Byzantine failures. However, with these improvements, we believe most failures can now be handled smoothly via the new fast recovery paths.

References​